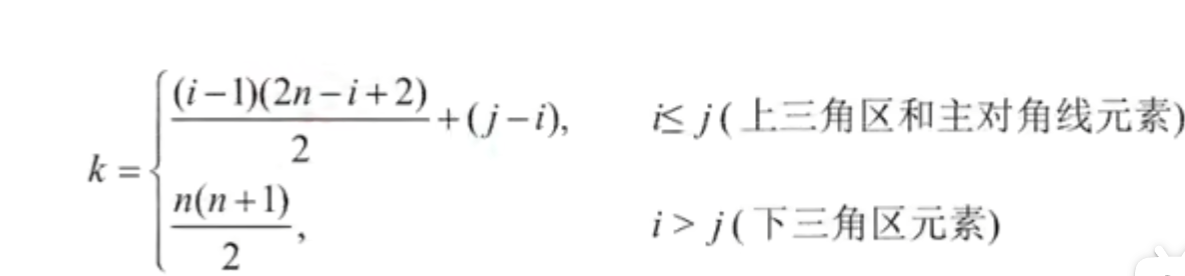数组和特殊矩阵的压缩储存

数组和特殊矩阵的压缩储存
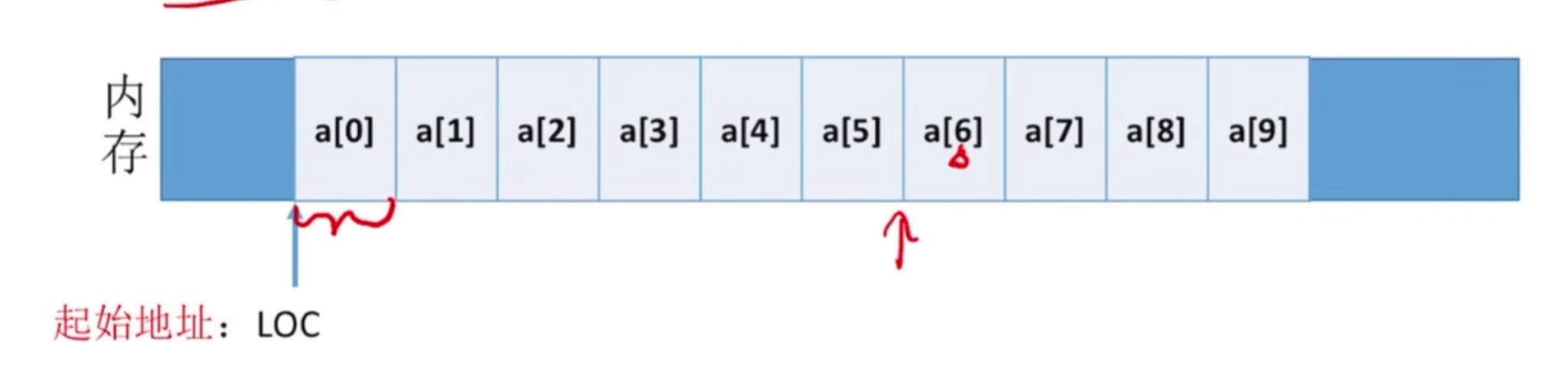
WhYqZz一维数组的储存结构
C语言定义一维数组:ElemType a[10]
各数组元素大小相同,且物理上连续存放
数组元素a[i]的存放地址=LOC+i*sizeof(ELemType)(0<=i<=10)
二维数组的储存结构
C语言定义二维数组:ElemType b[2][4]
两种储存方式
- 行优先储存
M行N列的二维数组b[M][N],若按照行优先存储
则b[i][j]的存储地址=LOC+(i*N+j)*sizeof(ElemType) - 列优先储存
M行N列的二维数组b[M][N],若按照列优先存储
则b[i][j]的存储地址=LOC+(i+j*M)*sizeof(ElemType)
普通矩阵的存储
$\left(\begin{array}{cccccc}
a_{1,1} & a_{1,2} & a_{1,3} & \cdots \cdots & a_{1, n-1} & a_{1, n} \\
a_{2,1} & a_{2,2} & a_{2,3} & \cdots \cdots & a_{2, n-1} & a_{2, n} \\
a_{3,1} & a_{3,2} & a_{3,3} & \cdots \cdots & a_{3, n-1} & a_{3, n} \\
\vdots & \vdots & \vdots & & \vdots & \vdots \\
a_{m, 1} & a_{m, 2} & a_{m, 3} & \cdots \cdots & a_{m, n-1} & a_{m, n}
\end{array}\right)$
可用二维数组存储
注:描述矩阵元素时,行号和列号一般从1开始,而描述数组时一般从0开始(具体看题目的条件)
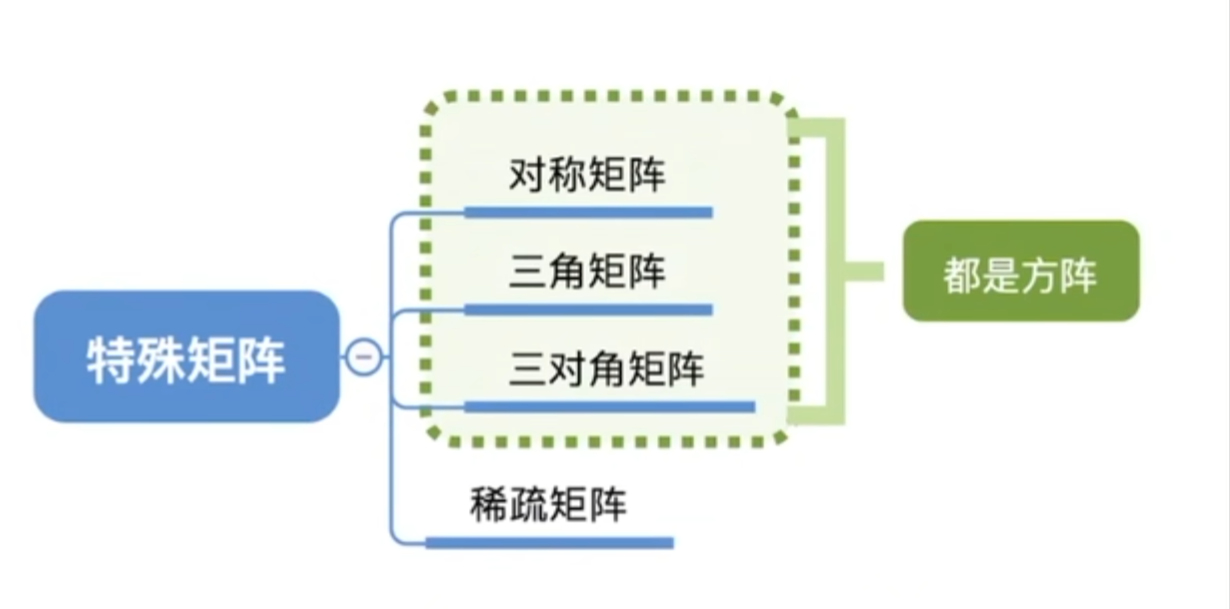
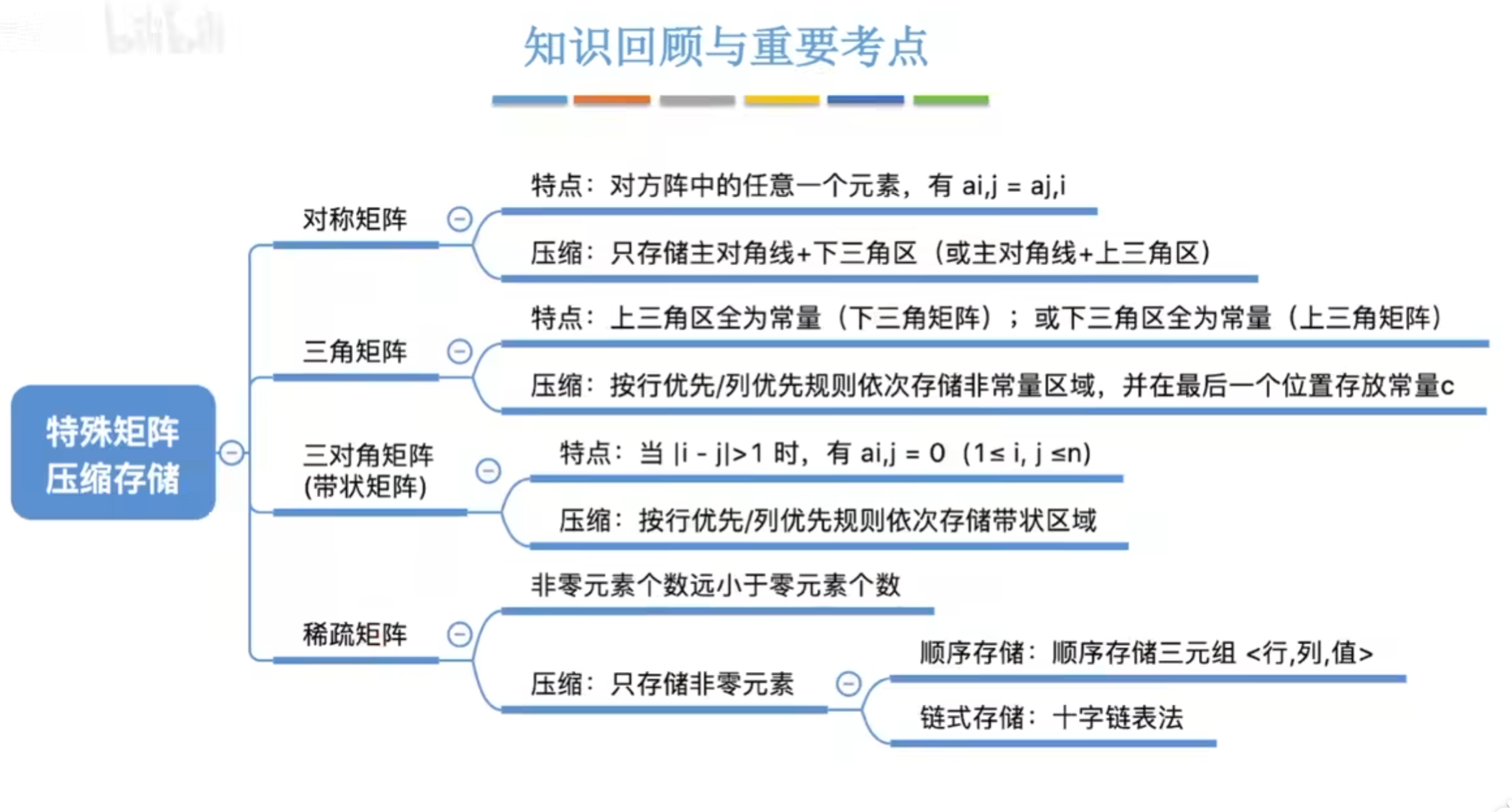
某些特殊矩阵可以压缩存储空间
对称矩阵的压缩存储
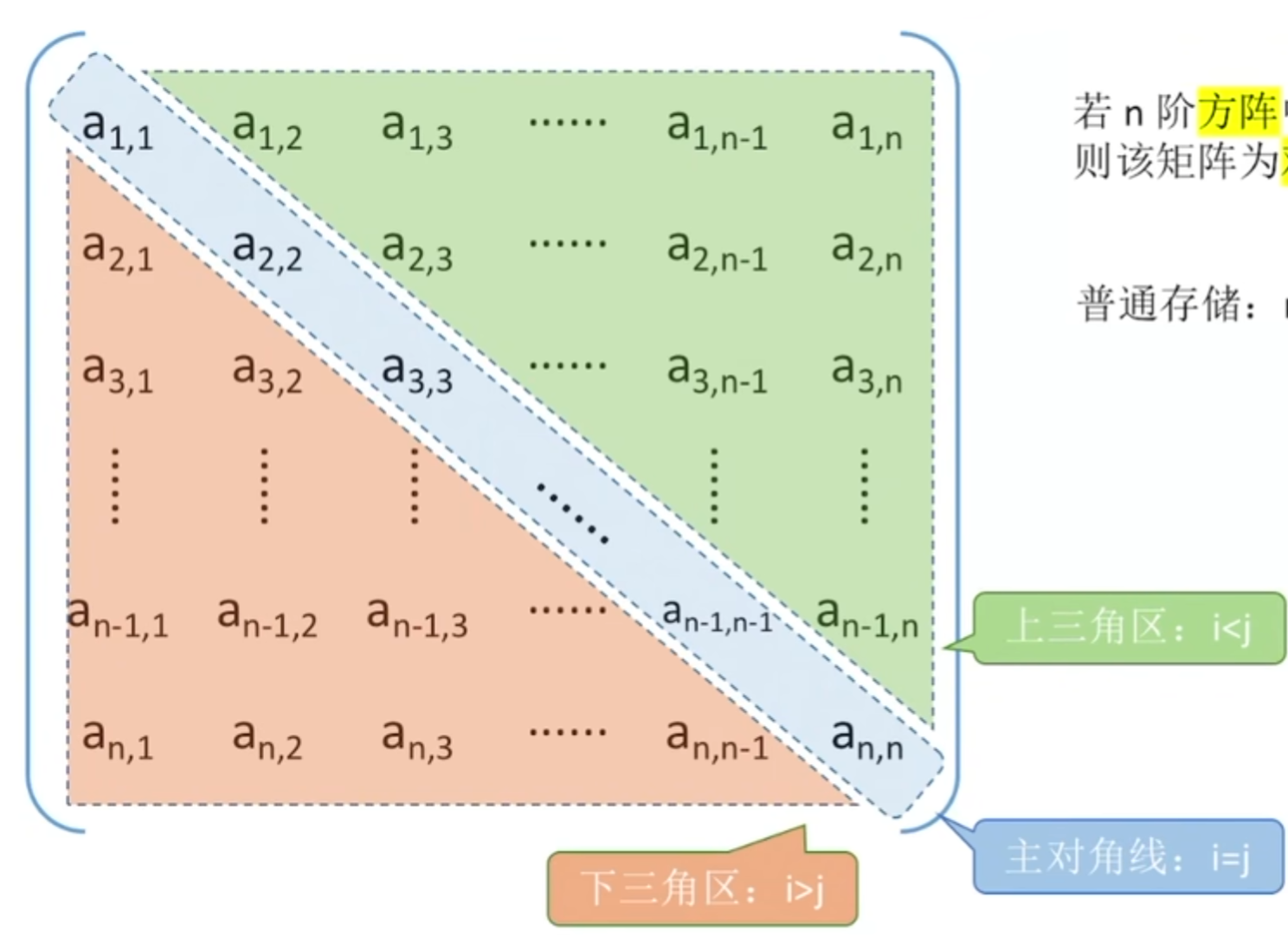
若n阶方阵中任意元素$a_{i,j}$,都有$a_{i,j}$=$a_{j,i}$,则该矩阵为对称矩阵
普通储存:n*n二维数组
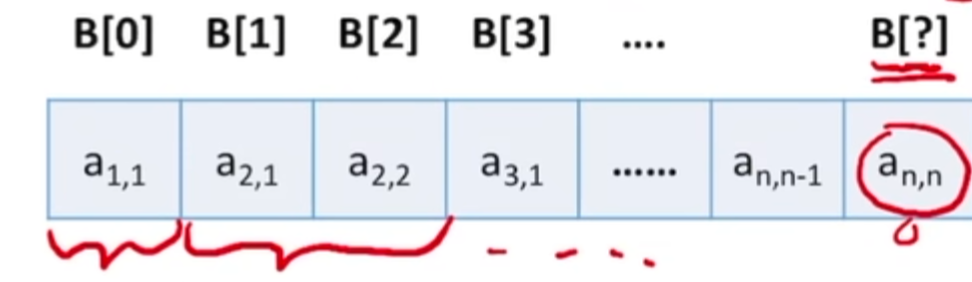
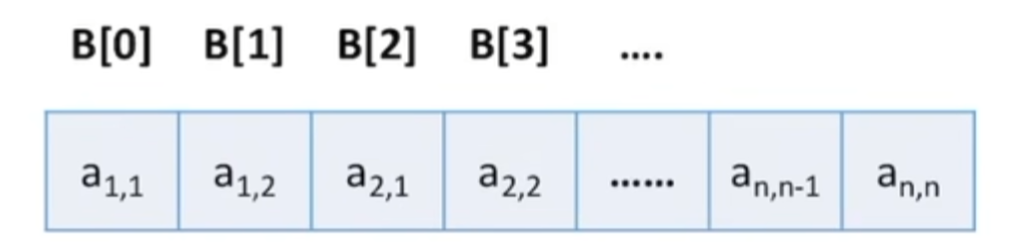
压缩存储策略:只储存主对角线和下三角区
- 按行优先原则将各元素存在一维数组中
- 数组大小
第一行:1个元素
第二行:2个元素
第三行:3个元素
…….
第n行:n个元素
等差数列求和:一共有(1+n)*n/2个元素
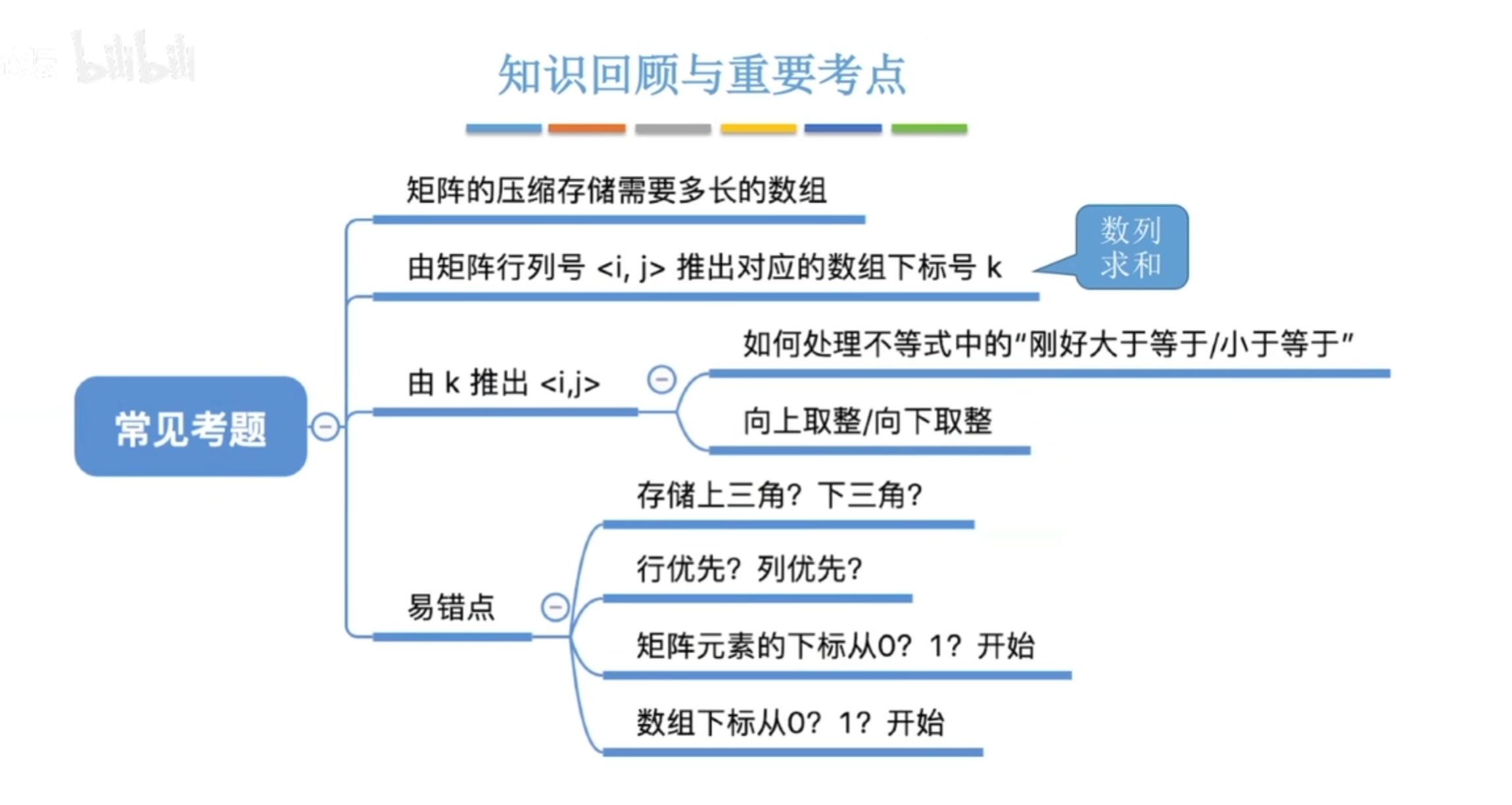
因为数组下标是从0开始的,所以B[?]==B[(1+n)*n/2]\ - 对称矩阵压缩后怎样才能方便使用
- 可以使用一个映射函数 矩阵下标——>一维数组下标 $a_{i,j}$(i<j)——>B[k]
- 按照行优先,$a_{i,j}$是第几个元素?
[1+2+…+(i-1)]+j——>第$\frac{i(i-1)}{2}$+j个元素——>数组下标k=$\frac{i(i-1)}{2}$+j-1
若(i>j),由于对称矩阵的性质,$a_{i,j}$==$a_{j,i}$
- 数组大小
- 按列优先原则: 矩阵下标——>一维数组下标
$a_{i,j}$前有1~j-1列
第一列:n个元素
第二列:n-1个元素
…….
第j-1列:n-j+2个元素
在同一列$a_{i,j}$前有i-j个元素
由于需要算出$a_{i,j}$是第几个元素,所以再+1
数组下标k=[n+n-1+…+(n-j+2)]+(i-j)+1
三角矩阵的压缩储存
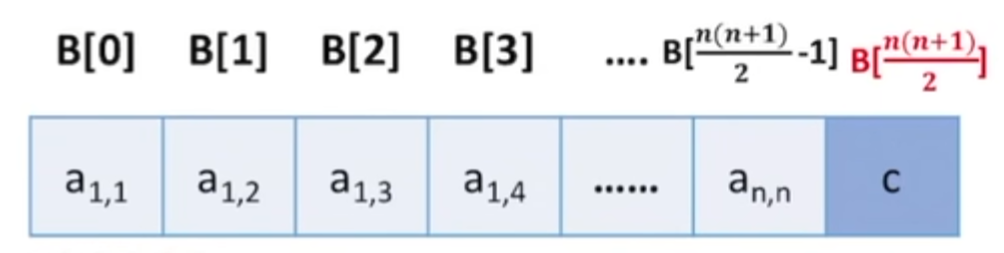
压缩储存策略:按照行优先原则将主对角线和上/下三角区元素存入一维数组中。并在最后一个位置储存常量。
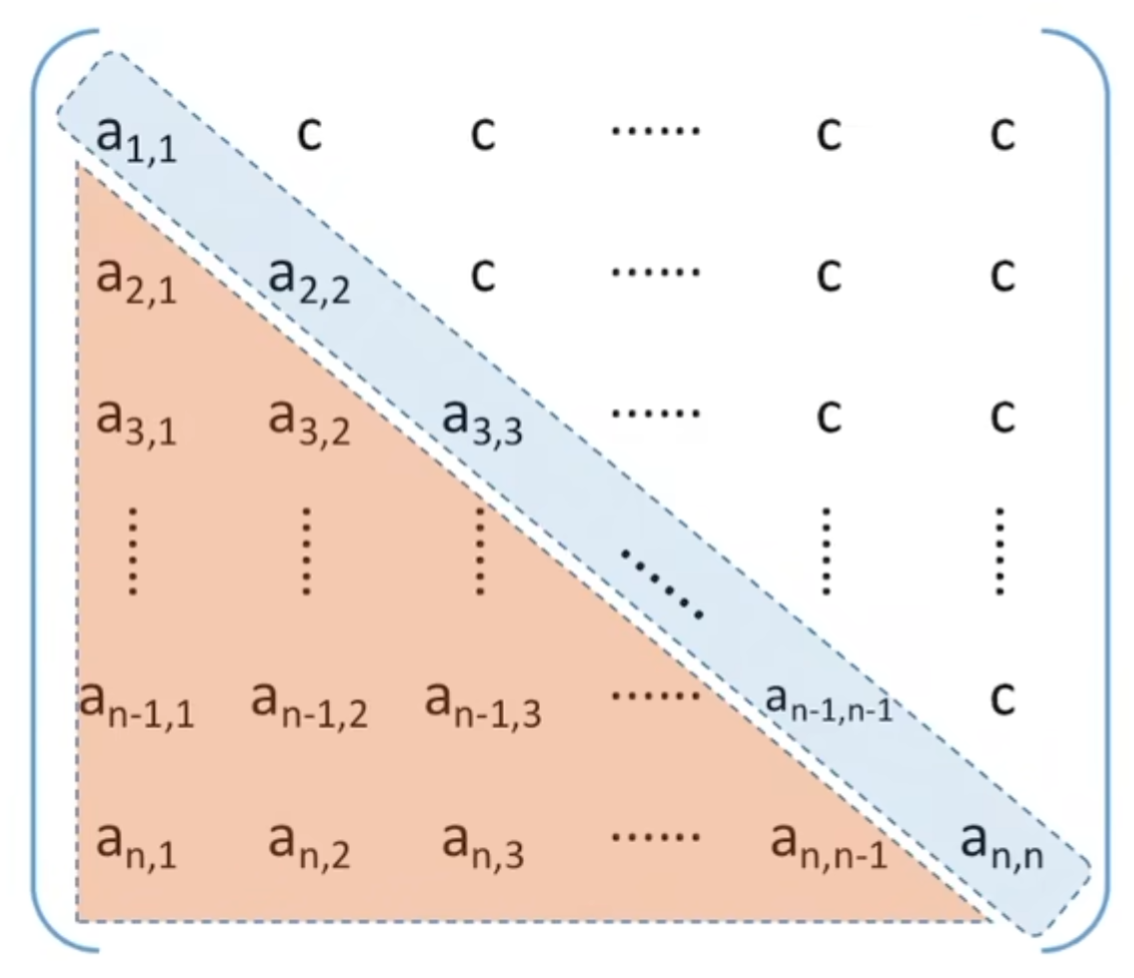
- 下三角矩阵:除了主对角线和下三角区,其他的元素都相同
- 数组大小为$\frac{n(n+1)}{2}+1$
- 按照行优先,$a_{i,j}$是第几个元素?
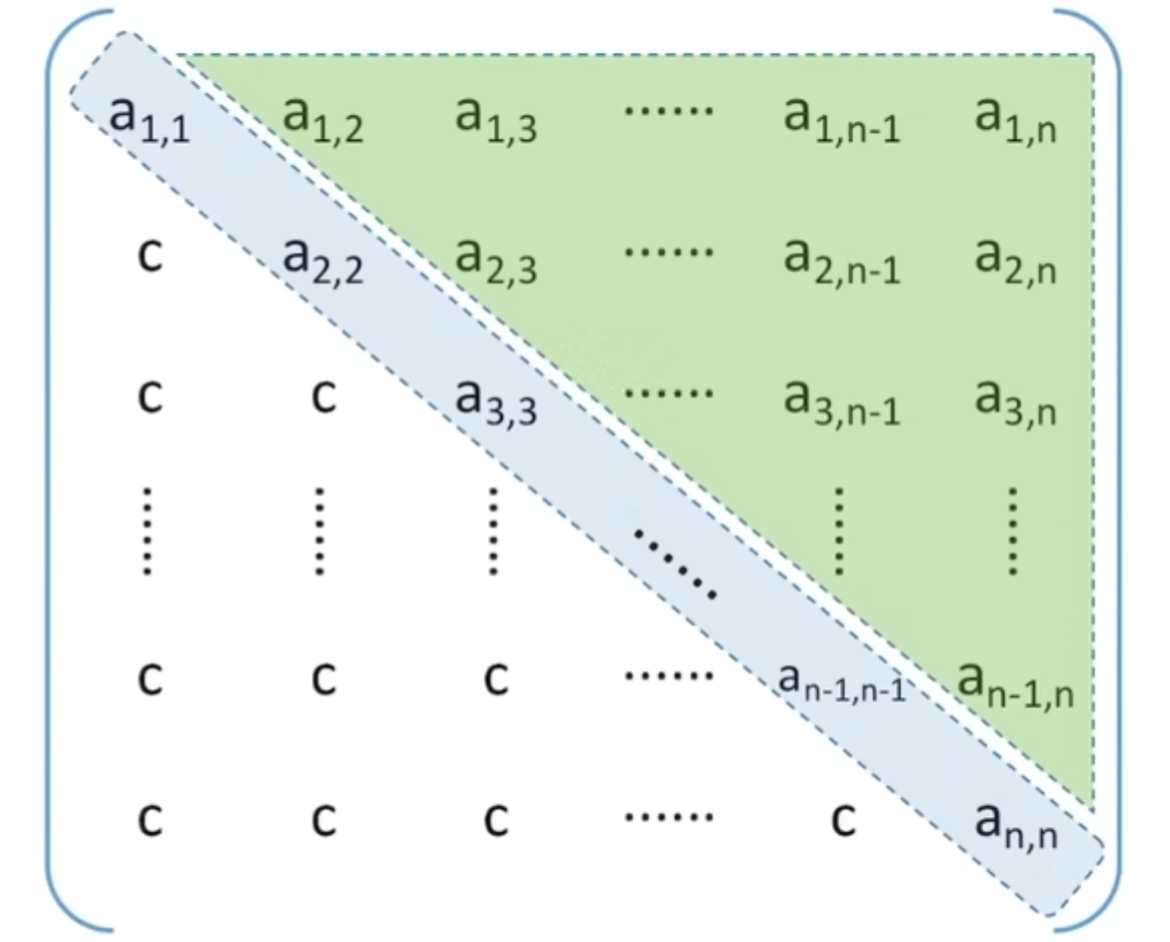
上三角矩阵:除了主对角线和上三角区,其他的元素都相同
- 按照行优先的原则,$a_{i,j}$是第几个元素
- 按照行优先的原则,$a_{i,j}$是第几个元素
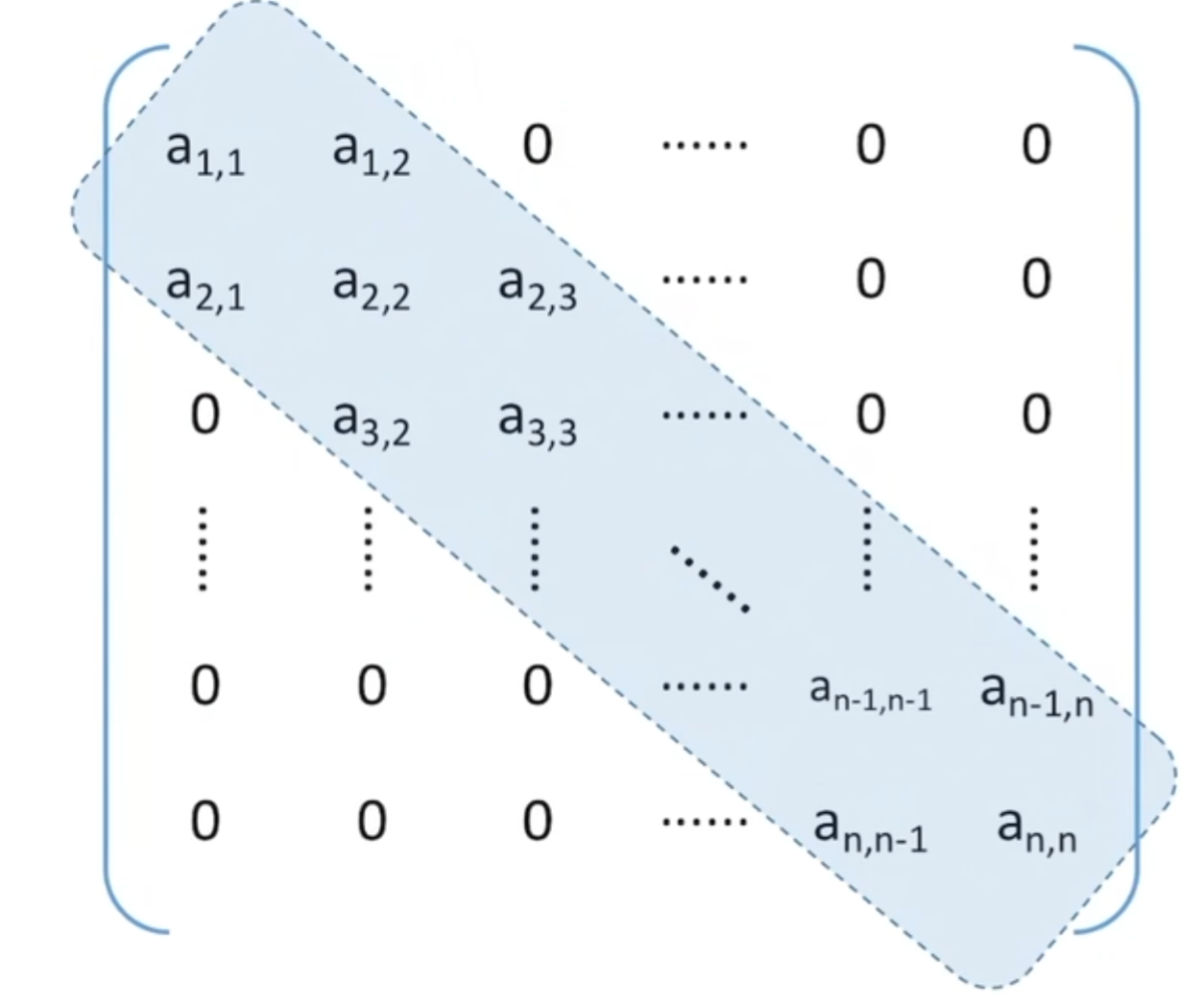
三对角矩阵的压缩储存
三对角矩阵,又称带状矩阵:当|i-j|>1时,有$a_{i,j}$=0(i>=1,j<=n)
压缩储存策略:按行优先/列优先原则,只储存带状部分
一维数组长度:3n-2(一行三个元素,第一行和最后一行各少一个元素)
- 按照行优先,$a_{i,j}$是第几个元素
前i-1行有3*(i-1)-1个元素,$a_{i,j}$是第i行的j-i+2个元素
$a_{i,j}$是第2i+j-2个元素
如过数组下标从0开始,那么数组下标k=2i+j-3 - 若已知数组下标k,如何得到i,j
第k+1个元素,在第几行,第几列
前i-1行有3(i-1)-1个元素,前i行有3i-1个元素
显然,$3(i-1)-1<k+1<=3i-1$
$i>=(k+2)/3$
$i=(k+2)/3$向上取整
由k=j-i+2得,j=k+2i-3
稀疏矩阵的压缩储存
稀疏矩阵:非零元素远远少于矩阵元素的个数
压缩储存策略:
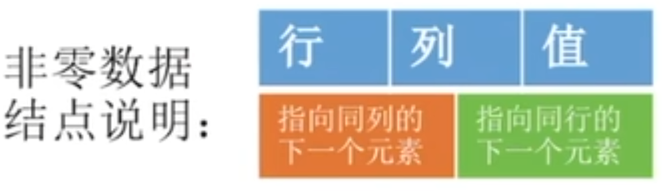
- 顺序储存——<行,列,值>
$\left(\begin{array}{llllll}
0 & 0 & 4 & 0 & 0 & 5 \\
0 & 3 & 0 & 9 & 0 & 0 \\
0 & 0 & 0 & 0 & 7 & 0 \\
0 & 2 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0
\end{array}\right)$i(行) j(列) v(值) 1 3 4 1 6 5 2 2 3 2 4 9 3 5 7 4 2 2
(此处行、列标,从1开始)
三元组可以定义一个struct,含有i、j、v
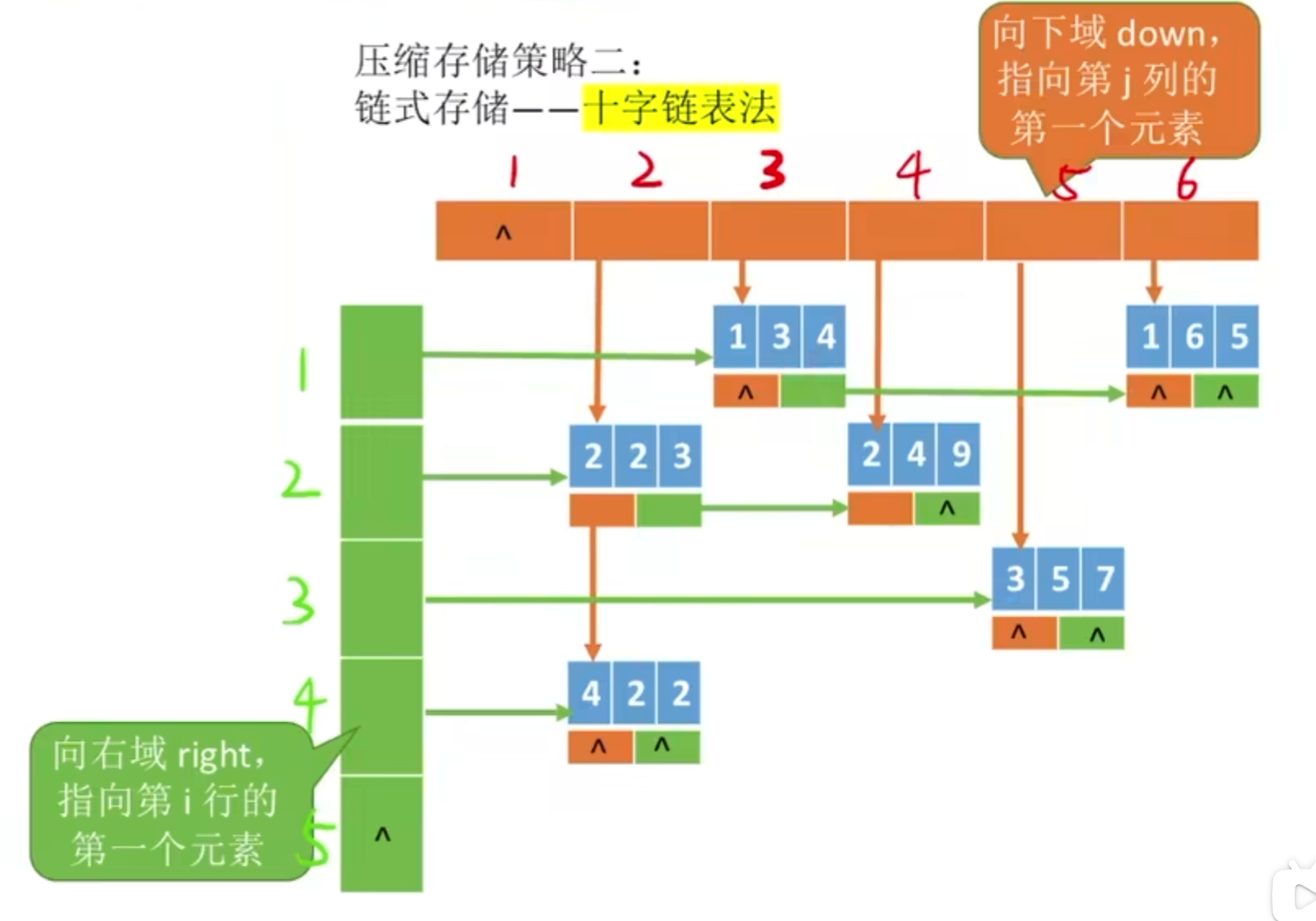
2. 链式存储——十字链表法