字符串模式匹配算法

字符串模式匹配算法
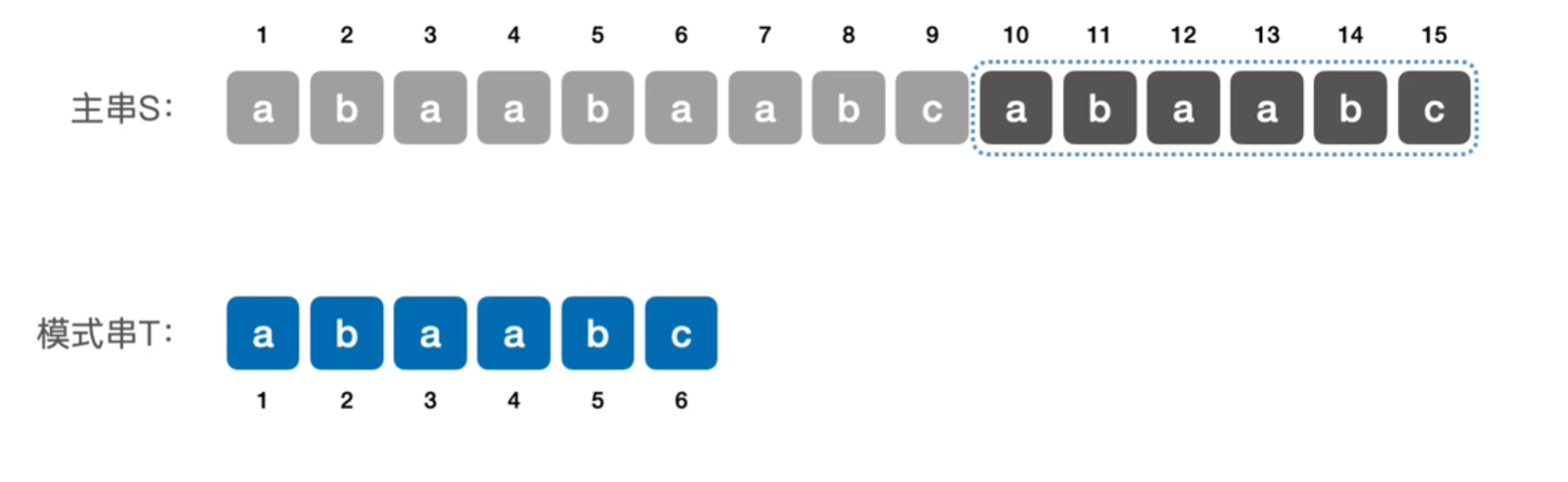
WhYqZz字符串模式匹配的定义
在主串中找出与模式串相同的子串,并返回其所在位置
朴素模式匹配算法
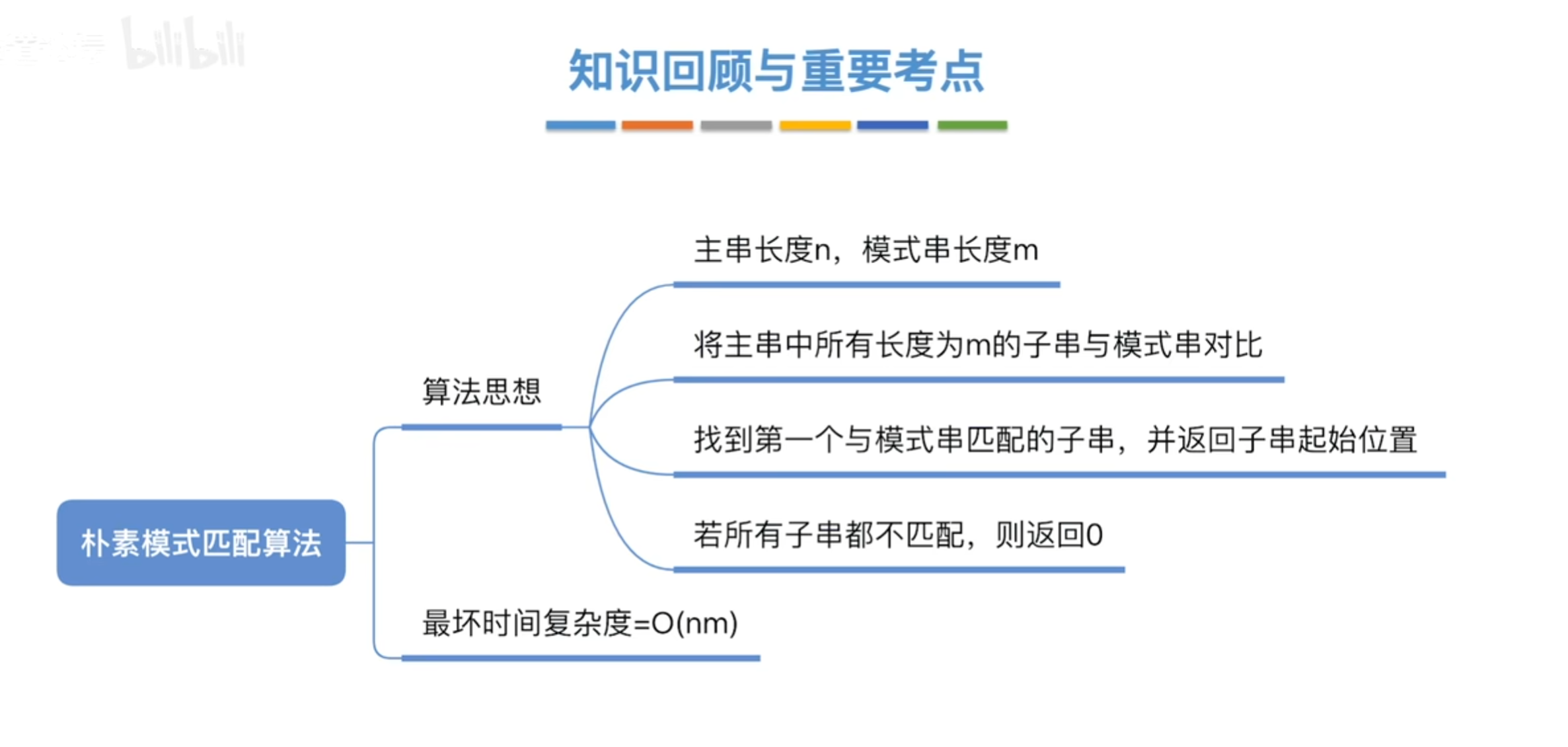
思想
主串长度为n,模式串长度为m
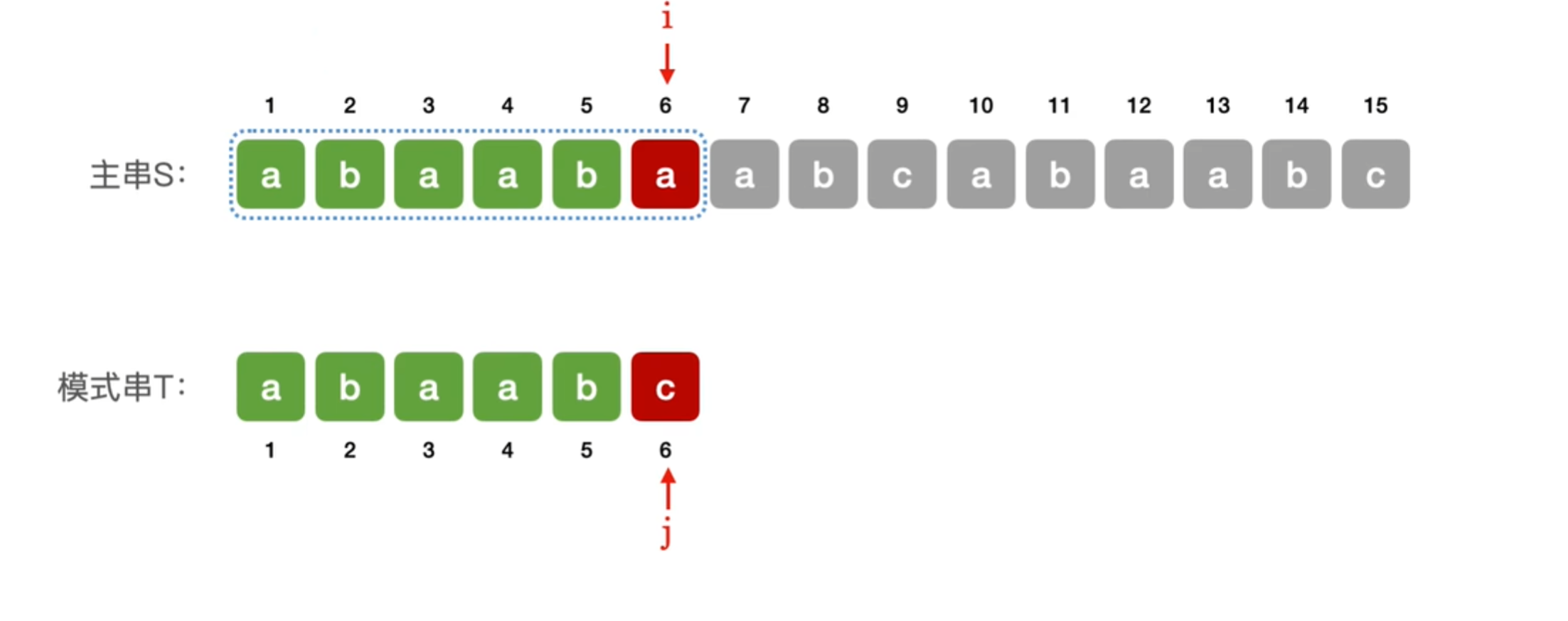
将主串中所有与长度为m的子串与模式串一一比较 ,直到找到一个与模式串完全匹配的子串,或所有的子串都不匹配 (最多对比n-m+1个子串)
若当前子串匹配失败,则主串指针i指向下一个子串的第一个位置,模式串指针j回到模式串的第一个位置i=i-j+2 j=1
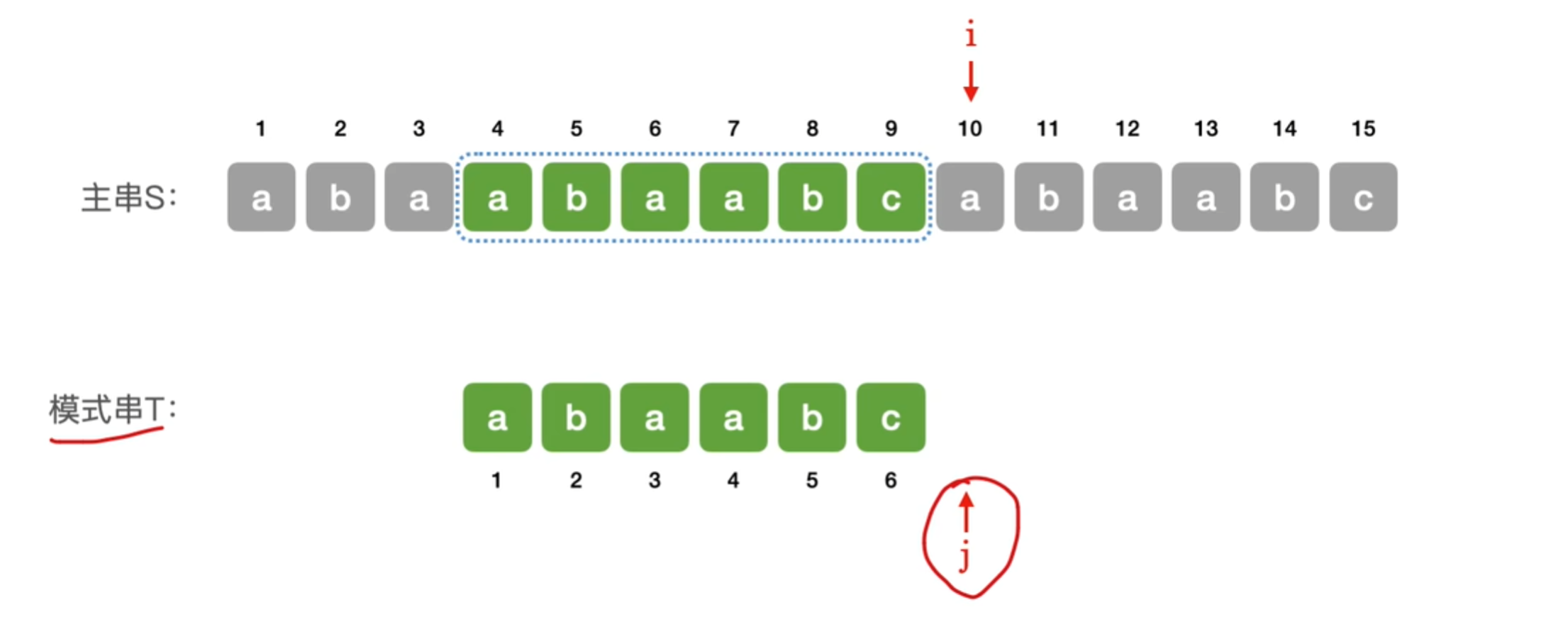
若j>T.length,则当前子串匹配成功,返回当前子串的第一个位置——i-T.length
代码
1 | int Index(SString S,SString T){ |
时间复杂度
朴素模式匹配算法时间复杂度$O(nm)$
缺点
当某些子串与模式串部分匹配的时候,主串的扫描指针i经常回溯,造成时间开销增大
知识回顾与重要考点
KMP算法
思路
主串指针不回溯,只有模式串指针回溯
如果j=k时才发现匹配失败,说明1~k-1都匹配成功
KMP算法的关键在于高出一个与模式串相对应的数组next
代码
1 | int KMP_Index(SString S,SString T,int next[]){ |
求模式串的next数组
思想
next数组:当模式串里的第j个字符匹配失败时,令模式串跳到next[j]再继续匹配
串的前缀:包含第一个字符,且不包含最后一个字符的子串
串的后缀:包含最后一个字符,且不包含第一个字符的子串
当第j个字符匹配失败,由1~j-1个字符组成的串记为S,则:
next[j]=S的最长相等前后缀长度+1
代码
- 求模式串的next数组
1
2
3
4
5
6
7
8
9
10
11
12
13void get_next(SString T,int next[]);{
int i=1,j=0;
next[1]=0;
while(i<T.length){
if(j==0||T.ch[i]==T.ch[j]){
i++;
j++;
//若pi=pj,则next[j+1]=next[k]+1
next[i]=j
}
else j=next[j];
}
} - KMP算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16int Index_KMP(SString S,SString T){
int i=1,j=1;
int next[T.length+1];
get_next(T,next);
while(i<S.length&&j<T.length){
if(j==0||S.ch[i]==T.ch[j]){
i++;
j++;
}
else{
j=next[j];
}
}
if(j>T.length)return i-T.length;
else return 0;
}
知识回顾与重要考点
朴素模式匹配算法的缺点:当某些子串与模式串能部分匹配时,主串的扫描指针i经常回溯,导致时间开销增加。
最坏时间复杂度O(nm)
KMP算法:当子串和模式串不匹配时,主串指针i不回溯,模式串指针j=next[j]
算法平均时间复杂度:O(n+m)
next数组手算方法:当第j个字符匹配失败,由前1~j-1个字符组成的串记为S,则:
next[j]=S的最长相等前后缀长度+1
特别地,next[1]=0,next[2]=1
next数组的优化
求nextval数组
1 | nextval[1]=0; |
| 序号j | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 模式串 | a | b | a | b | a | a |
| next[j] | 0 | 1 | 1 | 2 | 3 | 4 |
| nextval[j] | 0 | 1 | 0 | 1 | 0 | 4 |
评论
匿名评论隐私政策