并查集

WhYqZz2025-10-272025-11-05

并查集的逻辑结构

集合：将各个元素划分为若干个互不相交的子集
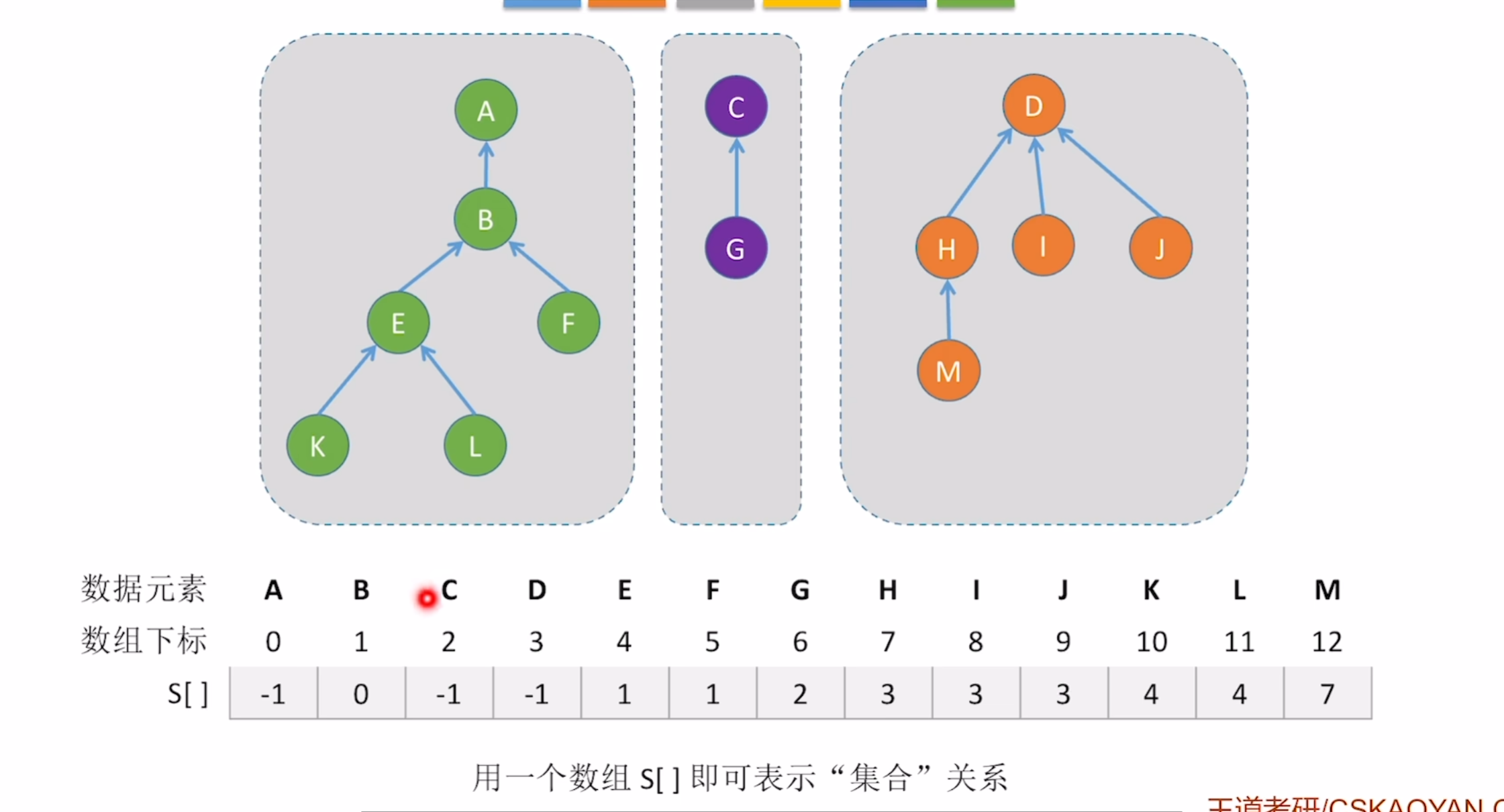
回顾：森林是多个互不相交的树的集合
所以可以用互不相交的树来表示多个集合

并查集的存储结构

本质上运用了树的双亲表示法

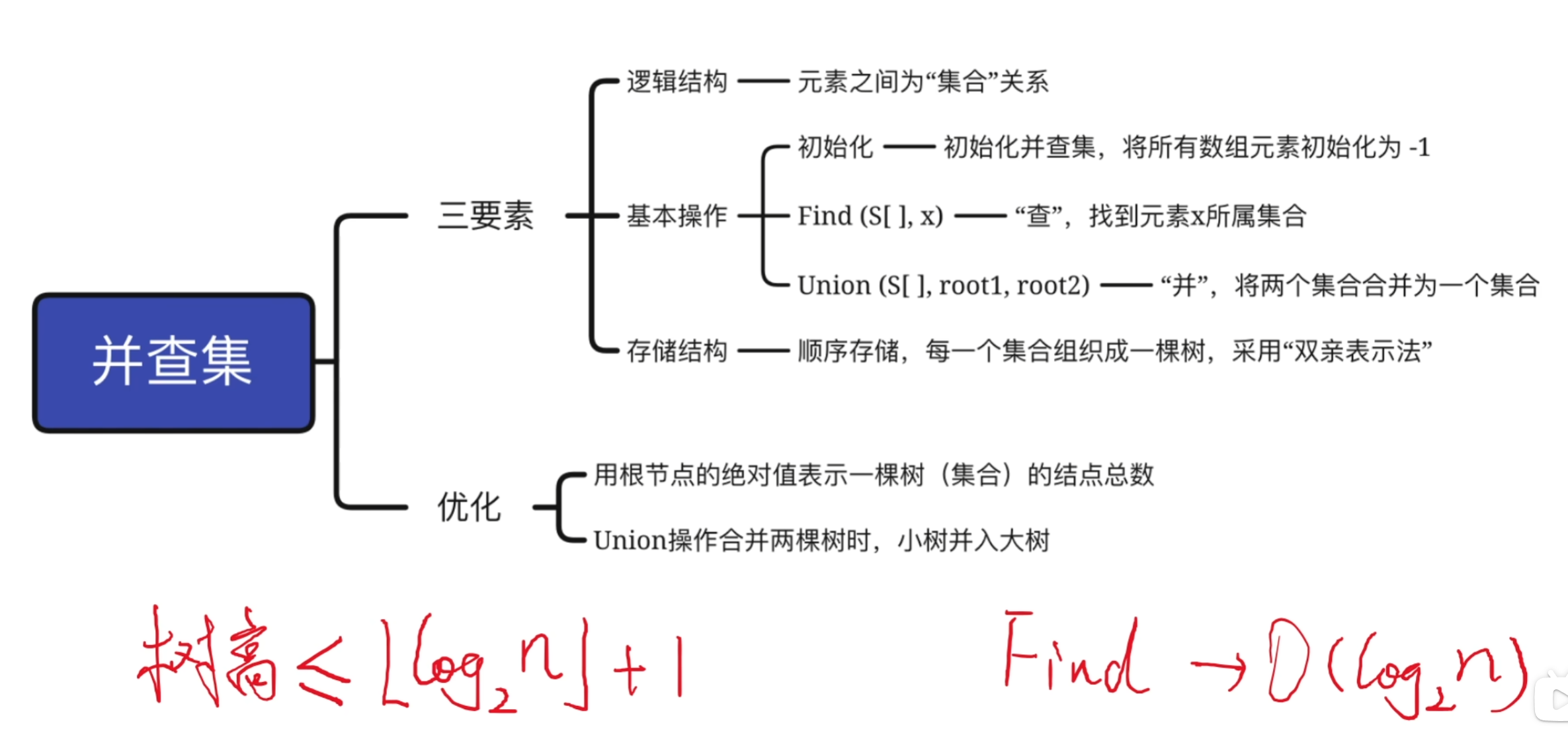
并查集的基本操作

查——Find：
确定一个指定元素的所属集合
并——Union：
将两个不相交的集合合并为一个

注：并查集是逻辑结构——集合的一种具体实现，只进行并和查两个基本操作

并查集的代码实现

#define SIZE 13
int UFSets[SIZE];
void Initial(int S[]){
    for(int i=0;i<SIZE;i++){
        S[i]=-1;
    }
}

查

int Find(int S[],int x){
    while[S[x]>=0]{
        x=S[x];
    }
    return x;
}

并

void Union(int S[],int Root1,int Root2){
    if(Root1==Root2)return;
    //将Root1连接到另一条根Root2下方
    S[Root2]=Root1;
}

若只给出两个元素，需要先进行Find操作找出根结点

Union操作的优化

思路：每次实现并的操作时，尽可能不让树长高

用根节点的绝对值表示树的结点总数

Union操作，让小树合并到大树

void Union(int S[],int Root1,int Root2){
    if(Root1==Root2)return;
    if(S[Root1]>S[Root2]){//Root1结点数量更少
        S[Root1]+=S[Root2]//累加结点总数
        S[Root1]=Root2;//小树合并到大树
    }
    else{
        S[Root2]+=S[Root1];
        S[Root2]=Root1;
    }
}

该方法构造的树高不超过[$\log_{2}{n}$]+1

知识回顾与重要考点

并查集Find操作的优化(压缩路径)

压缩路径——Find操作，先找到根结点，再将查找路径的所有结点都挂在根结点下

int Find(int S[],int x){
    int root=x;
    while(S[root]>=0)root=S[root];
    while(x!=root){
        int t=S[x];
        S[x]=root;
        x=t;
    }
    return root;
}